Verbreitete Aussagen zum Epidemieverlauf
Während er Corona-Epidemie gibt es einige immer wiederkehrende Aussagen in den Medien:
- Während der initialen Phase wächst die Anzahl der Infektionen exponentiell an. Um das zu veranschaulichen, wird von der – im Prinzip gleichbleibenden – Verdoppelungszeit gesprochen.
Diejenigen, die sich besonders wissenschaftlich ausdrücken willen, sprechen von dem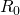 -Faktor (initiale relative Ansteckung), der zunächst immer größer wird.
-Faktor (initiale relative Ansteckung), der zunächst immer größer wird. - Diejenigen, die den Gesamtverlauf modellieren, sprechen von und visualisieren den Krankheitsverlauf mit einer Glockenkurve. Dies ist die aus der Statistik wohlbekannte Gauß-Verteilung
Dieser Beitrag dient dazu, mit einer einfachen Methode, der Oberstufenmathematik zugrundelegt, beide Modelle anhand realer Daten hinsichtlich ihrer Gültigkeit zu überprüfen, mit dem Ergebnis, aus den Originaldaten die entscheidenden Information zu erhalten, anstatt über hypothetische Modelle zu spekulieren.
Die Anregung zu diesem Beitrag bekam ich durch ein Interview mit dem Nobelpreisträger Prof. Michael Levitt, der in einer frühen Phase des Covid19-Ausbruchs in Wuhan die dortigen Fallzahlen untersuchte.
Test des exponentiellen Wachstums:¶
Liegt ein exponentielles Wachstum vor, folgen die Infektionszahlen y der Exponentialfunktion in Abhängigkeit von der Zeit t und einem konstanten Anpassungsfaktor ![]() .
.
![]()
Die Änderung einer Funktion wird durch deren Ableitung beschrieben, bei der Exponentialfunktion ist die Ableitung wieder eine Exponentialfunktion:
![]()
Mit diesem elementaren Wissen gibt es einen einfachen Test, ob eine zeitliche Sequenz von Daten einem exponentiellen Wachstum folgt – der Quotient aus Ableitung und Funktionswert, d.h. die relative Änderung muss zu jedem Zeitpunkt konstant sein:
![]()
Also wenn an einem Tag 100 Fallzahlen sind, und 50 neue dazukommen (50%, also ![]() ), kommen bei exponentiellem Wachstum zu dem neuen Wert 150 am darauf folgenden Tag wieder 50% dazu, was dann 225 ergibt, usw.
), kommen bei exponentiellem Wachstum zu dem neuen Wert 150 am darauf folgenden Tag wieder 50% dazu, was dann 225 ergibt, usw.
Auch bei exponentiell abnehmenden Fallzahlen ergibt sich für die relativen Änderungen eine Konstante, die allerdings negativ ist.
Die entscheidende Frage ist, ob und ggf. wie lange ein solches exponentielles Wachstum tatsächlich stattfindet?
Test der Glockenkurve¶
Die Glockenkurve ist das Modell, um den Gesamtverlauf der Epidemie zu beschreiben, insbesondere um den „Lockdown“ zu rechtfertigen, der das Ziel hat, die „Kurve abzuflachen“, mit dem Argument, das Gesundheitswesen nicht zu überfordern: Der kritische Höhepunkt der Epidemie ist erreicht, wenn täglich nicht mehr neue Fälle als am Vortag dazukommen. Von da an bleibt der Bedarf an medizinischen Resourcen absehbar, d.h. mit einer gewissen zeitlichen Verzögerung, begrenzt.
Hier eine vereinfachte Darstellung einer „Gaußglocke“ mit der Standardabweichung ![]() :
:
![]()
Die Ableitung davon ist:
![]()
Daraus ergibt sich für die relative Änderung, also für das Verhältnis von Ableitung zu Funktionswert:
![]()
Dies ist eine fallende gerade Linie mit der Steigung ![]() .
.
Diese Linie hat beim Maximum der Glockenkurve ihren Nulldurchgang.
Damit eignet sich wiederum die aus den Daten direkt bestimmbare Meßgröße ![]() optimal dafür, um zu prüfen, inwieweit die erhobenen Daten einer Glockenkurve entsprechen. Dazu muß aus den gemessenen Daten die mathematische Ableitung
optimal dafür, um zu prüfen, inwieweit die erhobenen Daten einer Glockenkurve entsprechen. Dazu muß aus den gemessenen Daten die mathematische Ableitung ![]() berechnet werden.
berechnet werden.
Berechnung der Ableitung aus diskreten Datenpunkten¶
Strenggenommen kann man von nicht-kontinuierlichen Daten keine Ableitung bestimmen, denn es ist ein „schlecht gestelltes“ Problem. Eine naive Näherung ist, einfach die Differenzen benachbarter Zeitpunkte zu berechnen. Da die Daten aber nicht „sauber“ sind und z.T. mit großen Fehlern behaftet (an Wochenenden wird viel weniger gemessen als unter der Woche), sind bei dem naiven Ansatz die Fehler durch Artefakte größer als die Daten, für die man sich interessiert.
Die Lösung dieses Problems erreicht man durch „Regularisierung“, indem die Meßdaten durch gewichtete Mittelung der benachbarten Daten geglättet werden, bevor die Differenzen zu den Nachbarn gebildet werden.
In den Modellen des RKI wurden z.B. gleitende Mittelwerte von je 4 Tagen verwendet. Es ist allerdings bewiesen, dass die Bildung von unerwünschten Artefakten bei Verwendung einer Gaußfunktion zur Glättung am geringsten ist. Diese wird bei diskreten Daten durch Binomialkoeffizienten optimal angenähert, z.B. bei einer Mittelung mit Hilfe von 5 Datenpunkten werden diese mit (1,4,6,4,1)/16 gewichtet. Die hier verwendeten Mittelungen nutzen allerdings sehr viel mehr Nachbarn (etwa 20-30).
Die Umgebungsgröße ist ein freier Parameter. Sie wird hier relativ groß gewählt, um die Fehler der Datenerfassung weitgehend zu eliminieren. Wer in den Nachrichten aufmerksam zugehört hat, wird in den letzten Tagen (Anfang Mai) gehört haben, dass das RKI entschieden hat, die Daten mehr zu glätten, um einen zuverlässigeren Schätzwert des Reproduktionsfaktors ![]() zu erhalten (es waren aufgrund von Artefakten infolge geringer Glättung die täglich erhobenen Reproduktionsfaktoren von Deutschland kurzzeitig über 1, was zu den bekannten irrationalen Panikreaktionen von Medien und Bundeskanzlerin führte, siehe auch hier).
zu erhalten (es waren aufgrund von Artefakten infolge geringer Glättung die täglich erhobenen Reproduktionsfaktoren von Deutschland kurzzeitig über 1, was zu den bekannten irrationalen Panikreaktionen von Medien und Bundeskanzlerin führte, siehe auch hier).
Um zu verhindern, dass der Nenner von ![]() zu 0 wird, wird vorsichtshalber zu den gemessenen Daten von
zu 0 wird, wird vorsichtshalber zu den gemessenen Daten von ![]() noch 1 dazugezählt, es wird also strenggenommen
noch 1 dazugezählt, es wird also strenggenommen ![]() berechnet. Dies beeinflusst das Ergebnis nur minimal.
berechnet. Dies beeinflusst das Ergebnis nur minimal.
RKI-Daten von Deutschland
Das folgende Diagramm zeigt die täglichen deutschen Covid19-Fallzahlen, wie sie vom Robert-Koch-Institut (RKI) veröffentlicht werden, zusammen mit der oben beschriebenen Glättungstechnik und zum Vergleich die RKI-Glättungstechnik (gleitender Mittelwert). Das RKI hat große Sorgfalt darauf verwandt, das wahre Anfangsdatum der Erkrankung in jedem Erkrankungsfall abzuschätzen, bevor die Signalverarbeitung angewandt wird. Die Methode wird „Nowcasting“ genannt und trägt wesentlich zu einer deutlich verbesserten Datenqualität bei.
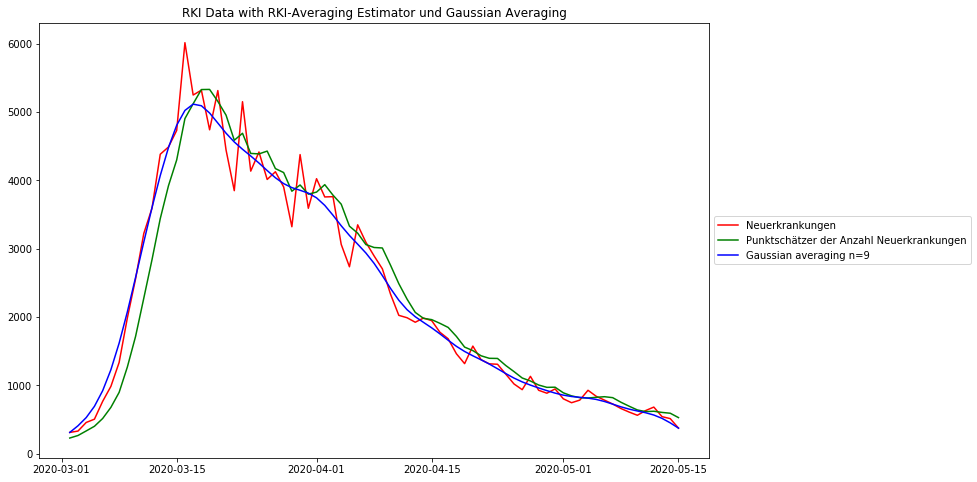
Beide Mittelungsverfahren eliminieren das „Rauschen“, die Gaußsche Glättung mehr als die RKI-Methode. Es ist zu beobachten, dass die RKI-Glättung die Daten um 3-4 Datenpunkte systematisch nach rechts, also in die Zukunft, verschiebt. Das sollte nicht sein und es verfälscht daraus abgeleitete zeitliche Aussagen.
Ein mögliches Problem der starken Gaußschen Glättung ist, dass die Spitze etwas niedriger erscheint als mit dem RKI-Schätzer. Aber abgesehen von der höheren Datentreue ist die Position des Maximums viel besser erhalten als mit dem RKI-Schätzer.
Darstellung der relativen Änderungen
Das Diagramm zeigt die relativen Veränderungen pro Tag für die deutschen RKI-Daten. Wie oben diskutiert, beschreiben diese Daten die Art des stattfindenden Wachstums.
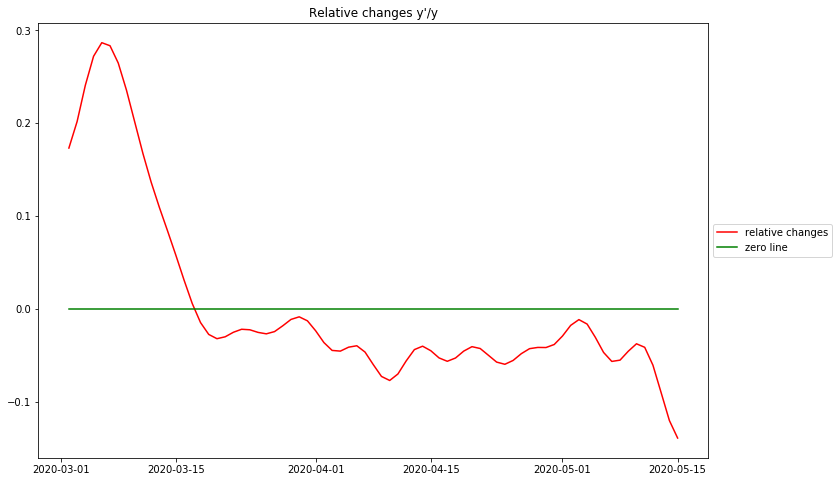
Es gibt im wesentlichen 3 identifizierbare Phasen: Die erste aufsteigende Phase vor dem Höhepunkt steht ganz am Anfang der Epidemie. Aufgrund der Tatsache, dass in diesem Datensatz keine Zahlen vor dem 1. März 2020 verfügbar sind, ist es zweifelhaft, ob es sich dabei um ein Artefakt der Datenverarbeitung oder um ein reales Phänomen handelt. Andere vollständigere Datensätze deuten darauf hin, dass die Epidemie bei der maximalen relativen Veränderung beginnt – dem entspricht die maximale Reproduktionsrate ![]() zu Beginn der Epidemie.
zu Beginn der Epidemie.
Die größte Überraschung ist, dass es keine Phase exponentiellen Wachstums gibt, wie man an dem ziemlich spitzen Höhepunkt erkennen kann. Für exponentielles Wachstum müsste dies ein Plateau sein. Stattdessen fällt die Kurve ziemlich stark ab, mit dem Verlauf einer Geraden, und kreuzt am 16. März 2020 den Nullpunkt. Dies ist der Tag, an dem die täglichen Original-Falldaten ihren Maximalwert erreichen – dies ist der Tag, an dem die „Kurve abgeflacht“ wird, an dem die Zahl der neuen Fälle zu sinken beginnt. Aus der vorangegangenen Diskussion deuten diese Beobachtungen stark darauf hin, dass der ansteigende Teil der Epidemiekurve sehr genau einer Glockenkurve folgt. Es muss hier festgehalten werden, dass der vollständige Prozess des Erreichen des Maximums der Fallzahlen und des Rückgangs der Neuerkrankungen erreicht wurde, bevor die strengen Maßnahmen in Deutschland eingeführt wurden (am 23. März 2020).
Nach dem Höhepunkt der Fälle ist die relative Veränderung in Deutschland strikt unter 0 geblieben. Offensichtlich nimmt die Kurve nicht mehr linear ab wie vor dem Überschreiten von 0, d.h. der Rest der Kurve ist keine Glockenkurve mehr. Die beste einfache Annäherung kann mit einem konstanten Wert knapp unter 0 gemacht werden. Dies entspricht einem langsamen exponentiellem Abfall der Fallzahlen.
Der Umstand, dass in Deutschland die relativen Änderungen vor dem gewaltsamen Anhalten eines großen Teils der Volkswirtschaft und des Zusammenlebens unter 0 waren und während der gesamten Zeit dieser Maßnahmen etwa auf demselben Wert geblieben sind, läßt große Zweifel an der Sinnhaftigkeit der politischen Panikreaktionen aufkommen. Es gibt nur eine vernünftige Deutung der Daten des RKI: Nach Bekanntwerden der ersten Fälle waren die Menschen bereits von sich aus so umsichtig, dass bereits vor allen Zwangsmaßnahmen der hierzulande bestmögliche Infektionsschutz erreicht war. Dieser wurde durch die Zwangsmaßnahmen nicht besser, was man am waagrechten Verlauf der relativen Änderungen erkennen kann. Erst nach der „Lockerung“ Anfang Mai ist eine weitere Senkung der relativen Änderungen erkennbar.
Offenbar ist auch eine Abteilung im Innenministerium zu ähnlichen Erkenntnissen gekommen, die Beteiligten wurden dafür aber zum Schweigen gebracht.
Abschätzung des R-Wertes¶
Ein Schlüsselelement in der Diskussion über eine Epidemie ist der sogenannte Reproduktionswert R, d.h. die Anzahl der Personen, die von einer zuvor infizierten Person infiziert sind. Dieser spielt auch bei der Modellierung der Ausbreitung der Epidemie eine wichtige Rolle. Das Robert-Koch-Institut hat einen Algorithmus entwickelt, um den R-Wert direkt aus den Fallzahlen zu messen. Hier möchte ich ihren Schätzer diskutieren und ihn mit meinem Ansatz zur Analyse der Daten in Beziehung setzen.
Der folgende Abschnitt ist mathematisch etwas herausfordernd, aber er ist notwendig, um meine Behauptung zu begründen, dass die resultierende Formel tatsächlich ein korrekter Schätzer der Reproduktionszahl R ist. Denjenigen, die Zweifel an der Gültigkeit der Formel am Ende dieses Abschnitts haben, wird allerdings empfohlen, den ganzen Abschnitt lesen.
Das Konzept des Robert-Koch-Instituts zur Schätzung des zeitlichen Verlauf des R-Wertes besteht darin, das Verhältnis zweier um 4 Tage auseinanderliegenden geglätteten Falldaten ![]() zu berechnen:
zu berechnen:
![]()
Sowohl Glättungsoperation des RKI als auch das Verhältnis zwischen den geglätteten Daten verschieben das Ergebnis nach rechts, d.h. zu späteren Zeitpunkten. Dies ist meines Erachtens falsch, weil es das Ergebnis verfälscht, denn
- Eine Glättung sollte niemals Zeitverschiebungen von Daten bewirken. Das bedeutet, dass für eine zeitliche Glättung auch Daten aus der Zukunft herangezogen werden.
- Wenn die Reproduktionszahl R die Ursache für die Zunahme oder Abnahme von Fallzahlen ist, darf diese Ursache niemals in der Zukunft liegen. Im äußersten Fall ist
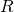 gleichzeitig mit der Veränderung, die sie verursacht. Diese Philosophie wird durch die Ableitung der Funktion dargestellt, wobei die Änderung direkt am Datenpunkt selbst gemessen wird.
gleichzeitig mit der Veränderung, die sie verursacht. Diese Philosophie wird durch die Ableitung der Funktion dargestellt, wobei die Änderung direkt am Datenpunkt selbst gemessen wird.
Mit den publizierten Daten des RKI lässt sich leicht nachweisen, dass das Datum der maximalen Fallzahlen (16.3.2020, Maximum der „nowcasted“ täglichen Infektionen – „Datum des Erkrankungsbeginns“) nicht mit dem Unterschreiten des Wertes 1 der R-Werte aus den RKI-Daten zusammenfällt. (das müßte dann spätestens am 17.3.2020 geschehen) Dieser kritische Wert wird 5-6 Tage später gemeldet (je nach Grad der Glättung – „Punktschätzer der Reproduktionsrate/Punktschätzer des 7 Tage R-Werts“).
Deshalb modifiziere ich den Ausdruck, um ihn zeitsymmetrisch zu machen (dies ändert nur die Zeitverschiebung, nicht die Funktionswerte), und verwende das (n-mal) geglättete Datenfeld ![]() als Datenquelle :
als Datenquelle :
![]()
Bildung des (natürlichen) Logarithmus hiervon macht aus dem Quotienten eine Differenz:
![]()
Mit ![]() als Ausgangsdaten wird deren Ableitung als Differenz der rechten und linken Nachbarn berechnet:
als Ausgangsdaten wird deren Ableitung als Differenz der rechten und linken Nachbarn berechnet:
![]()
Aufgrund der Glattheit durch die Vorverarbeitungf zwischen ![]() und
und ![]() kann für diese 5 Punkte mit Sicherheit angenommen werden, dass sie auf einer geraden Linie liegen, so dass die Differenz zwischen den Werten an den Punkten (t+2) und (t-2) etwa doppelt so groß ist wie die Wertdifferenz zwischen (t+1) und (t-1). Deshalb ist
kann für diese 5 Punkte mit Sicherheit angenommen werden, dass sie auf einer geraden Linie liegen, so dass die Differenz zwischen den Werten an den Punkten (t+2) und (t-2) etwa doppelt so groß ist wie die Wertdifferenz zwischen (t+1) und (t-1). Deshalb ist
![]()
und schließlich
![]()
Das folgende Diagramm zeigt die berechneten ![]() und gleichzeitig die publizierten RKI
und gleichzeitig die publizierten RKI ![]() Daten, um 5 Tage nach links, d.h. in die Vergangenheit, verschoben:
Daten, um 5 Tage nach links, d.h. in die Vergangenheit, verschoben:
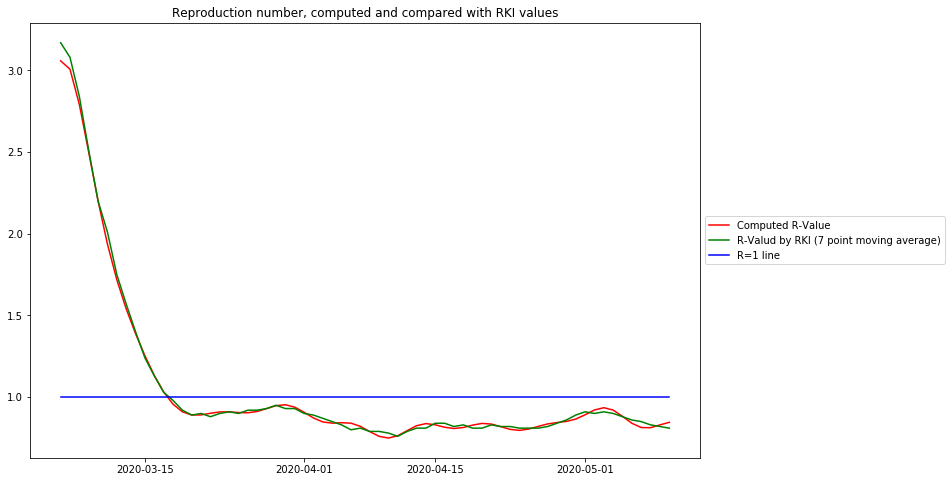
Aus diesem Diagramm können folgende Schlussfolgerungen gezogen werden:
- Die auf der Gaußschen Glättung und Ableitung basierende Kurve gibt exakt den R-Wert des Robert-Koch-Instituts wieder
- Die leicht verständliche relative Änderung der Falldaten steht in engem Zusammenhang mit dem R-Wert:
- Der R-Wert visualisiert besser die epidemiologische Ursache – eine Person infiziert R andere
- Die relative Änderung ist besser geeignet, um zu modellieren und vorherzusagen, weil sie sich auf bekannte mathematische Funktionen bezieht.
- Der R-Wert zwischen seiner Spitze und dem Überschreiten der Linie für den Wert 1 ähnelt ebenfalls einer Kurve nahe einer Geraden, und er kreuzt die Linie für den Wert 1 an derselben Stelle, an der sich der Nulldurchgang des relativen Änderungswertes befindet. Daher werden für qualitative Auswertungen die öffentlich bekannteren R-Daten zu Demonstrationszwecken verwendet. Für modellbasierte Vorhersagen sind die relativen Änderungsdaten besser geeignet.
Verlauf in Deutschland¶
Um den Verlauf in Deutschland mit den anderen Ländern vergleichen zu können, wird dieser hier noch einmal mit den Daten der John-Hopkins Universität dargestellt. Daraus ist unmittelbar ersichtlich, daß die Datenqualität des RKI um Klassen besser ist als die der John-Hopkins Universität. Das ist m.E. vor allem auf das beim RKI angewandte Verfahren des „Nowcasting“ zurückzuführen, wonach versucht wird, bei jedem Einzelfall das Datum des Erkrankungsbeginns zu rekonstruieren. Dies bereinigt die Daten von den Zufälligkeiten der Datenerhebung.
Interpretation der Diagramme¶
Die Rohdaten sind extrem „verrauscht“, d.h. es gibt Tage, an denen gar keine Fallzahlen auftreten. Es sind auch deutlich die wöchentlichen Erfassungsmuster erkennbar. Die geglätteten Kurven geben den intuitiv erwarteten Verlauf gut wieder.
Die Diagramme der relativen Änderungen zeigen, dass es keine Phase mit ungebremstem exponentiellen Wachstum gab, an keinem einzigen Ort. Mit ungebremstem Wachstum gäbe es beim absoluten Maximum der Kurven der relativen Änderungen ein Plateau.
Das Maximum der momentanen Änderung liegt in jedem Fall am Anfang der Epidemie, wenn die Fallzahlen noch sehr klein sind. Die Änderungsrate, die mit der Ansteckungsrate zusammenhängt, sinkt sehr schnell. Der Grad der „Gefährlichkeit des Ausbruchs“ hat offenbar mit der Höhe der initialen Änderungsrate zu tun. In Deutschland mit initial 40%/Tag war der Ausbruch bei weitem nicht so vehement wie in Italien oder New York, wo die initiale Änderungsrate etwa 60%/Tag betrug – zu einem Zeitpunkt, als man sich der Gefahr noch überhaupt nicht bewußt war.
Der Verlauf der Epidemie wird links vom Maximum der Meßdaten in den meisten Fällen gut durch eine Glockenkurve repräsentiert, d.h. die Kurve der relativen Änderungen wird zwischen deren Maximum und dem Nulldurchgang gut durch eine abfallende Gerade angenähert. Die Abweichungen von der Geraden bei den deutschen Fallzahlen lassen sich m.E. durch die schlechte Datenqualität des John-Hopkins-Datensatzes erklären.
Rechts vom Maximum der Meßdaten, also im Bereich fallender Werte, sind die relativen Änderungen konsequenterweise alle negativ. Ob dieser Bereich besser durch eine Konstante (exponentieller Abfall) oder durch eine ganz sanft fallende Gerade approximiert (Glockenkurve), läßt sich wahrscheinlich nicht generell sagen, vielleicht ergibt sich durch die Untersuchung von mehr Ländern noch ein klareres Bild.
Es ist insofern aber unerheblich, weil es für ein sicheres Ausklingen der Epidemie vor allem darauf ankommt, dass die relativen Änderungen unter 0 bleiben, je weiter, desto schneller geht es.
Schlussfolgerungen¶
Die Darstellung des Epidemieverlaufs mit Hilfe der ![]() Transformation erlaubt es, ohne ein „obskures“ Modell die wesentlichen Phasen des Epidemieverlaufs zu bewerten und sogar Prognosen zu machen. Das englische Modell des Imperial College, das den meisten initialen Prognosen zugrunde lag, hat offenbar 15000 Programmzeilen, die nach dem Verlassen des bisherigen Projektleiters Neil Ferguson niemand mehr nachvollziehen kann, und dessen Qualität mittlerweile angezweifelt wird.
Transformation erlaubt es, ohne ein „obskures“ Modell die wesentlichen Phasen des Epidemieverlaufs zu bewerten und sogar Prognosen zu machen. Das englische Modell des Imperial College, das den meisten initialen Prognosen zugrunde lag, hat offenbar 15000 Programmzeilen, die nach dem Verlassen des bisherigen Projektleiters Neil Ferguson niemand mehr nachvollziehen kann, und dessen Qualität mittlerweile angezweifelt wird.
Der initiale Anstieg bis zum Maximum der relativen Änderungen ist irrelevant und ein Artefakt der Glättung. Bei genauer Betrachtung fällt dieser Anstieg in einen Bereich der Originaldaten, in denen diese bei 0 oder fast bei 0 liegen, also vor dem zahlenmäßig relevanten erfaßten Beginn der Epidemie. Das bedeutet, dass die Verbreitungsrate bereits zu Beginn maximal ist und dass dieses initiale Niveau entscheidend ist für den weiteren Verlauf.
Durch Annäherung der ![]() Kurve nach dem Maximum mit einer Geraden läßt sich die voraussichtliche Position des Nulldurchgangs und damit der voraussichtliche Zeitpunkt des Erreichens der „flachen Kurve“ prognostizieren. Diese Möglichkeit hängt jedoch stark von der Qualität der ursprünglichen Daten ab.
Kurve nach dem Maximum mit einer Geraden läßt sich die voraussichtliche Position des Nulldurchgangs und damit der voraussichtliche Zeitpunkt des Erreichens der „flachen Kurve“ prognostizieren. Diese Möglichkeit hängt jedoch stark von der Qualität der ursprünglichen Daten ab.
In jedem Falle eignet sich diese Darstellung dafür, um offizielle Aussagen über den Politik-entscheidenden Reproduktionsfaktor ![]() zu überprüfen.
zu überprüfen.